A learnability analysis on neuro-symbolic learning

The learnability of a nesy task is decided by its DCSP solutions.

Recently, neuro-symbolic learning becomes a hot research topic, the researchers aim to unify data-driven machine learning and knowledge-driven logical reasoning within one hybrid framework, where both learning model and reasoning model are full-capacity. Representitive works including DeepProbLog and abductive learning.

A typical inference process of a hybrid neuro-symbolic system.

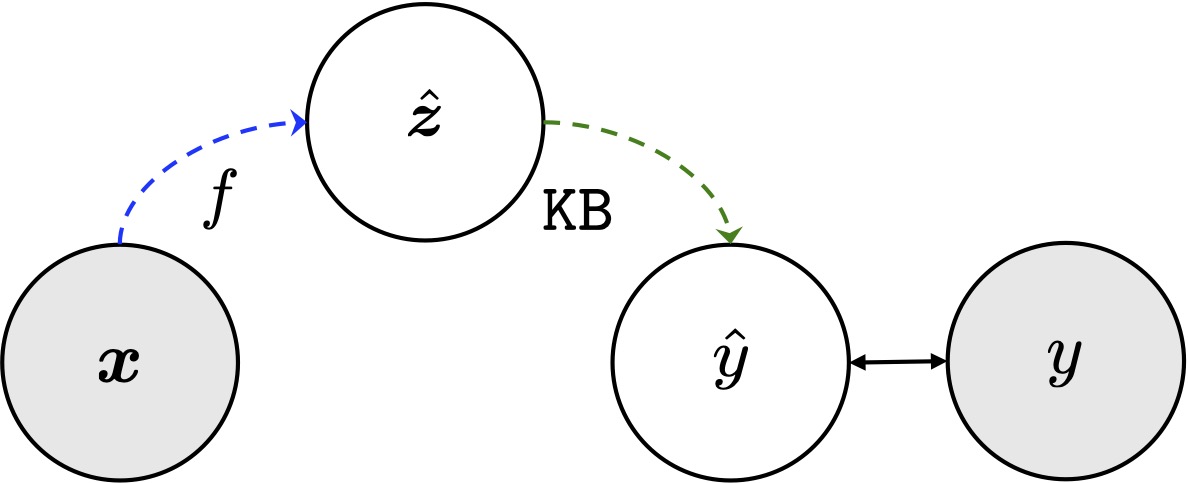
In this case, the system including a learning model $f: \mathcal{X} \mapsto \mathcal{Z}$, which mapping the raw data into concept space; and a reasoning model $\mathtt{KB}$ consist of rules which restrict on the concept space. Given the concept sequence $\boldsymbol{z} = (z_1, \dots, z_m)$, the knowledge base can imply a signal or target label $y$.

Usually, the training process of NeSy system is weakly-supervised manner, i.e., learning model $f$ with only $(\boldsymbol{x}, y)$ pairs and background knowledge $\mathtt{KB}$ to be satisfied.

The objective is to learn $f$ that generalise on concepts well:

\[R_{0/1} = \mathbb{E}_{(x, z)} \left[\mathbb{I}(f(x)\neq z) \right].\]

However, in the absense of supervision $\boldsymbol{z}$, only the surrogate nesy risk is accessible:

\[R_{nesy}(f) = \mathbb{E}_{(\boldsymbol{x}, y)}\left[ \mathbb{I}(f(\boldsymbol{x}) \land \mathtt{KB} \not\models y)\right].\]

The nesy risk can be further surrogated with weighted model counting (WMC) or with abduction.